A bit of background
I’m finally at the point of my PhD candidacy exam. The way it works in my department at BU is straightforward: you and 3 professors come up with a list of 75 papers (divided into 3 topics, each pertaining to their expertise and related to your research). The exam is to write two essay responses for each set of 25 papers within 2 hours (closed-book, obviously). In order to prepare, I decided to write practice essays that connect all the papers within each corpus. I’m posting them here in case I want to refer to some ideas in the future. I don’t expect anyone to read these, but just to cover my back: 1) these were written by memory and within a time limit, so they merely work as poorly-written and heavily constrained introductions to each topic; and 2) English is my second language, and it takes me multiple drafts to write something presentable. Sorry for the crudeness and potential mistakes.
These blog posts will broadly encompass my research interests:
Computational models of decision making
Behavioral and Neuroeconomics, with a focus on delay and effort discounting
MRI-based functional connectivity and individualized functional brain mapping
This first blog post is about evidence accumulation problems, foraging environments, and model based behavior (RL and temporal difference in particular). These blog posts will assume some level of familiarity with the literature.
The Essay
One of the most common experimental scenarios in the decision making literature is the “two alternative forced choice” (TAFC). As its name implies, participants engaged in TAFC are given two options with distinct values (economic decisions) or amounts of evidence (perceptual decisions), and their job is to select their preferred economic option or the alternative that is perceptually stronger. It is easy to relate to this type of choice, as we are often faced with alternatives that demand perceptual discrimination after evaluation of the available evidence.
Under the umbrella of TAFC, questions regarding evidence accumulation during perceptual decision making have been addressed in two overarching ways (Bogacz et al, 2006). On one hand, Drift Diffusion Models (DDM) propose that a single evidence trace is produced by the difference in the strength of the alternatives. Evidence accumulation models like the DDM are helpful in providing parameterized summaries of different aspects of behavior, such as thresholds that govern how quickly a decision is reached, or any initial biases towards one option (Bogacz et al, 2006; Krajbich and Rangel, 2011). Expansions to this basic relative model can take the form of single parameters (e.g. lambda) that control the degree of conservative or impulsive accumulation. Other forms include units inhibiting each other, inhibiting sequential competitors, or a combination of recurrent excitation versus feedback inhibition (i.e. pooled inhibition. See figure below, in part taken from Bogacz and colleagues). Contrasting this relative view are absolute (or race) models, in which independent accumulators track evidence without much direct interaction among them. Relative models whose units actively inhibit each other can be shown to reduce to simple DDM both when accuracy and response speed are demanded (Bogacz et al 2006).
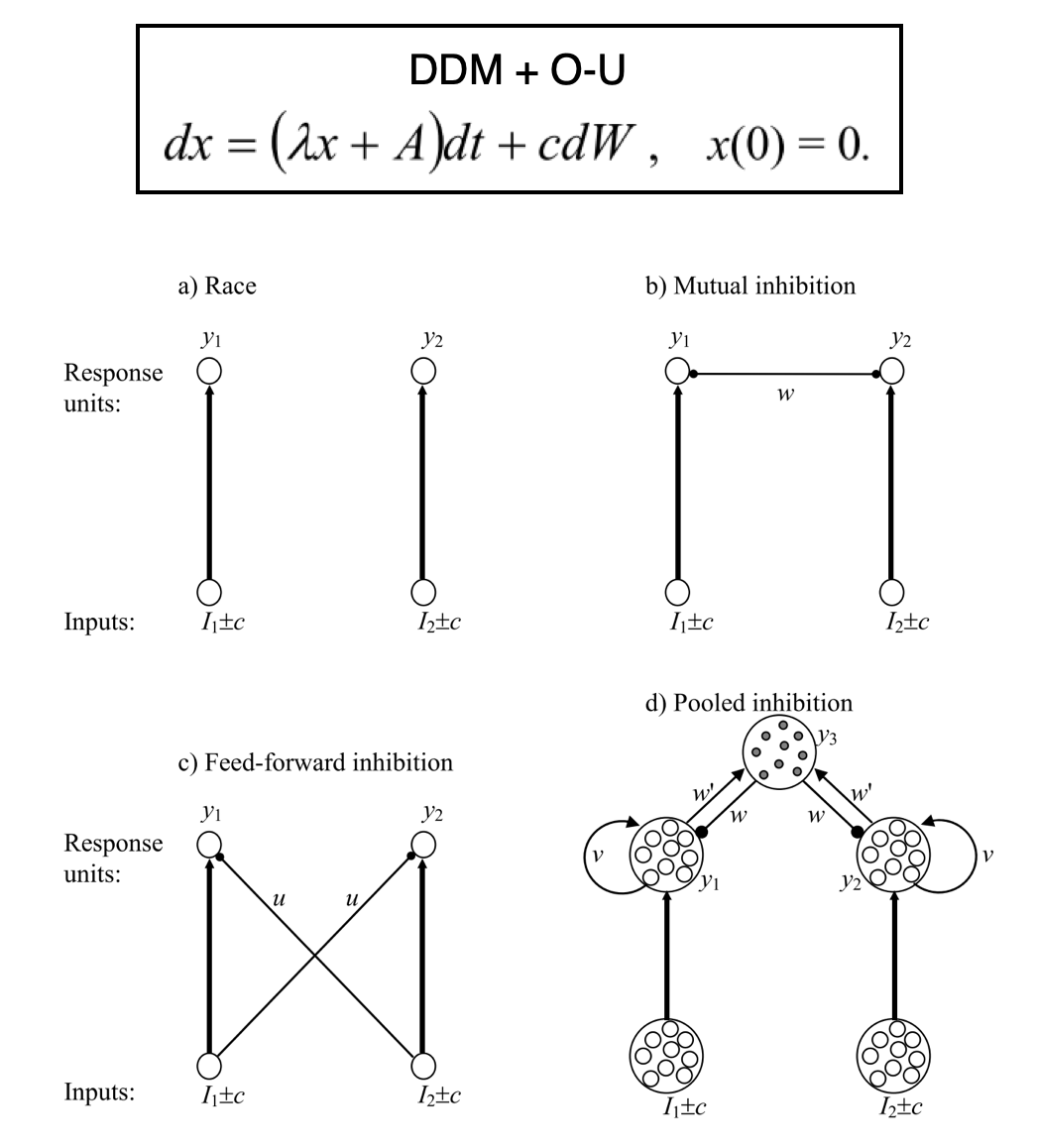
A limitation of traditional DDM is that model features (trace, threshold, bias, and lambda) are often inferred from response times, limiting our ability to zone in on what drives idiosyncrasies in evidence accumulation. To address this, Brunton et al (2013) created a translatable task in which animals and humans track discrete perceptual pulses presented at different rates per option (rather than following a continuous perceptual signal). Paired with a model that included a lambda term similar to O-U models (Bogacz et al., 2006), Brunton and colleagues found that the accumulation process in both species is noiseless (i.e. has perfect memory), and that noise in evidence tracking comes from sensory signals.
This type of DDM-style accumulation process finds neuroscientific support in the work of Roitman and Shadlen (2002). They recorded neuronal population activity in lateral intraparietal area (LIP) as rhesus monkeys completed a motion coherence task (directing their gaze towards the side where the highest percentage of dots were moving). They found that when most dots moved in the direction processed by the recorded hemisphere, neuronal activity steadily increased until a threshold was met. Notably, the higher the coherence (i.e. the stronger the evidence), the quicker the activity reached the threshold, even though post-threshold activity always followed the same activity rate. Moreover, coherence in the opposite direction produced mirroring inhibition in the recorded site. These dynamics resemble the relative accumulation process modeled by the DDM, particularly the mutual inhibition between competing processes (Bogacz et al, 2006). However, these results relied on surverying population dynamics, limiting our ability to argue that individual cells are tuned for DDM-style accumulation. To address this issue, Scott et al (2017) used calcium imaging to record individual neurons from the frontal orienting fields (FOF) and posterior parietal cortex (PPC). By taking advantage of the pulsatile TAFC design (Brunton et al., 2013), they showed that individual neurons have distinctive peak and spread of activity, and only show the canonical accumulator pattern when serially convolved with each other. Their findings give stronger evidence to absolute (i.e. race) models than the relative models covered so far, even though they showed weak mutual inhibition among neurons.
We can look at the idea of weakly-coupled inhibitors from a different perspective: divisive normalization (Louie, Khaw, and Glimcher 2013). This idea takes form after early perceptual processes where active neurons promote their information by also inhibiting their neighbors. When thinking of economic decisions, the authors propose that the value of each option is divided (normalized) by the aggregate value of the remaining options. This allows us to consider choices with multiple options, and introduces interesting effects (although Krajbich and Rangel (2011) have successfully expanded the DDM to trinary decisions by incorporating the value added by merely fixating on an item and reducing the question to a next-best comparison). For example, introducing a distractor item in a TAFC paradigm reduces the relative value of the original choices, but once the third item increases enough in value, the originally highest-valued option is boosted even more. This is seen in human and primate experiments, and reproduced by the mutual-inhibitor-like divisive normalization model. In fact, the model can be expanded to encompass multiple-trial valuation by pairing two pooled-inhibition populations, such that a slower population modulates the activity of the faster one across trials (Zimmerman, Glimcher, & Louie, 2018). This model successfully replicated animal and human findings showing that the range of values across trials determines the strength of the decision (embodied by the steeper sigmoidal describing the probabilities of choice). As mentioned above, the type of pooled inhibition with recurrent excitation configuration can be reduced to DDM (Bogacz et al, 2006). These findings seem at odds with the absolute models supported by findings from Scott et al (2017), which can also account for across-trial choice behavior. More work will be needed to align precise neuronal recordings with these behaviorally predictive models.
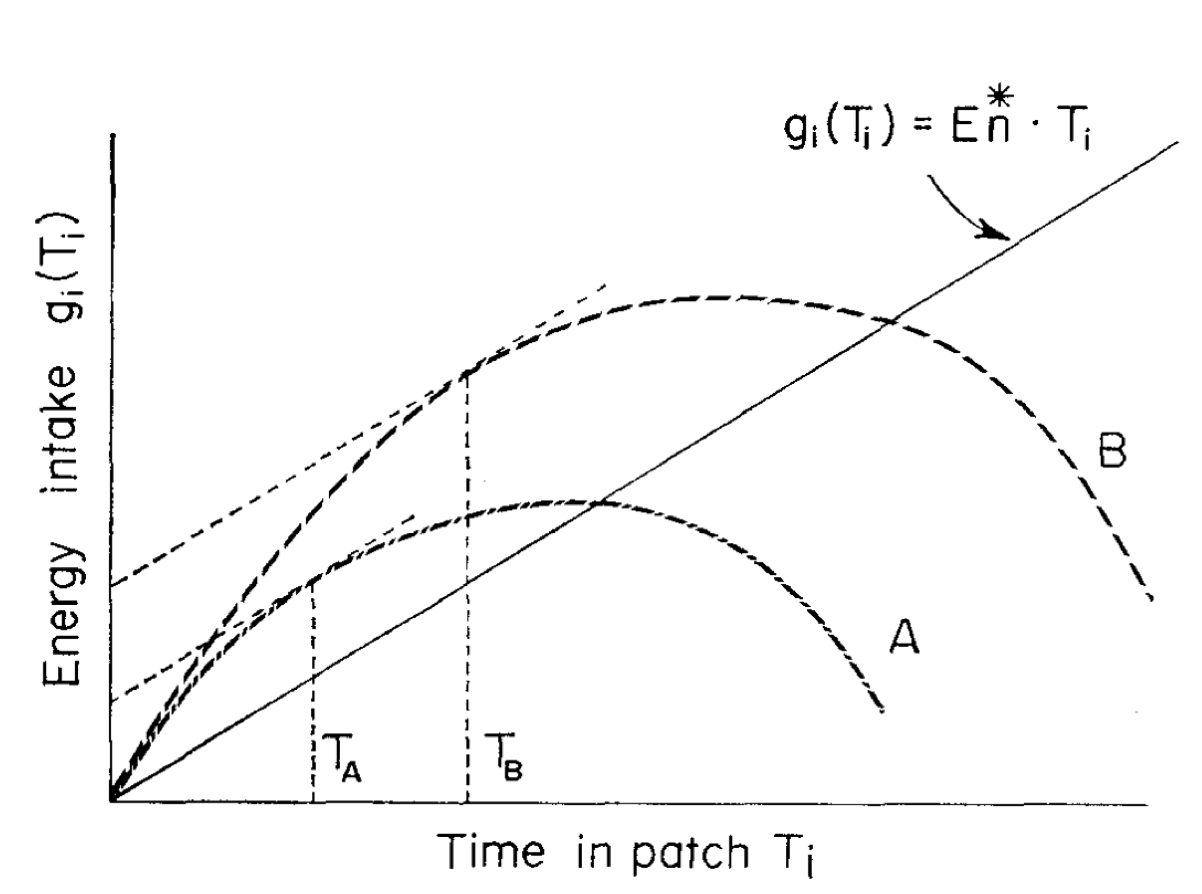
While many decisions involve a direct comparison among all the currently available options, we often face foraging-style, single-option sequential decisions with no immediate alternative outcomes. Foraging is an evolutionary pervasive behavior, and can manifest itself in simple ways, like when we decide to switch to a new job once we find that our current work is yielding diminishing gains. Traditional experimental and modeling work in foraging has focused on animal feeding patterns, and can be broadly divided into two. First, patch-style foraging in which an animal engaged in a depleting environment has to choose when to leave it in hopes for a richer one. And second, diet choice, in which the decision maker selects whether to engage with the current prey or search for a better alternative (note how the decision being emphasized is to leave in patches, but engage in prey selection). Unlike the more descriptive focus of accumulation models, foraging models tend to be normative. One of the first and most popular of these models is the “Marginal Value Theorem” (MVT; Charnov, 1976; Constantino & Daw, 2015), which states that animals should leave the current patch as soon as the instantaneous rate of gains falls below the habitat rate. The figure below shows Charnov’s original hypothetical derivation of the maximal rate of a habitat (solid line), and the peak of the earning rates for two patches. The tangent parallel to the solid line shows the point at which each patch yields a maximal rate of gains, after which animals should leave. This, of course, requires knowledge of the average reward depletion in the habitat. In terms of prey selection, Krebs et al (1977) established that animals facing poor environments (i.e. where profitable prey are rare) should be unselective, but as profitable prey become more common they should solely select them, despite what the relative rate of less profitable prey is. In both cases, the animal’s behavior should be governed by the opportunity cost of time (OC) incurred in persisting or engaging with their current environment.
Thinking about the environmental earning rate has important implications for TAFC as well, as the optimality of binary choices about the future often depends on what we can obtain from the environment while waiting (i.e. OC; Fawcett et al, 2012). For instance, selecting a smaller amount earned in a shorter period of time (compared to a larger-longer option) could be a long-term strategy to exit the trial in search for a more profitable one, rather than an impulsive preference for immediate rewards. However, a limitation of canonical foraging models is their focus on time as the most relevant guide of choice. Against this intuition, some work has shown that rats will overharvest areas with long delays that yield less than the OC, even when multiple timing environments are designed so that only the shortest trials should be accepted (Wikenheiser et al, 2013). This type of overharvesting is also seen in humans (Constantino & Daw, 2015; Davidson & Hady, 2019), and birds (Krebs et al., 1977), opening the door to many potential explanations of this phenomenon. Wikenheiser and colleagues attributed this unnecessary persistence to an aversion to rejecting, which was successfully added as a parameter to the canonical prey selection model. Curiously, rejection aversion positively correlated with OC, counterintuitively suggesting that rats are less selective when it pays to be so. Another theory that aims to account for this is called the “energy budget rule” (Krebs & Kacelnik, 1984), which emphasizes that choices depend on hunger and energy intake, not mere maximization of food acquisition rate. This becomes more important as the time horizon (i.e. the estimated foraging time; Fawcett et al., 2012) and satiety evolve during foraging, as seeking better alternatives actually becomes costlier than engaging with whatever is currently presented to them.
A similar explanation comes from Niv et al (2007). They argue that while phasic dopamine has been attributed to action selection and learning (see Schultz et al., 1997), tonic levels can be linked to the vigor of responses. This net dopamine concentration is said to reflect the opportunity cost of the environment, such that higher OC produces more vigorous responding. This vigor allows the animal to take advantage of the rich environment. Therefore, if the animal is full or an expected amount of reward has been achieved, all subsequent rewards lose attractiveness and the subjective OC decreases. This can produce overharvesting by increasing the relative cost of searching instead of sticking to the available patch or prey. Shifts in reference points over time have been observed in rats faced with gambles disclosed through pulses (Constantinople, Piet, & Brody, 2019), such that prospect-theoretic nonlinearities in subjective value flatten and low values become losses as experience recalibrates the reference point.
Regardless of their precise mechanism, a core weakness of traditional foraging models is their assumption that animals have full knowledge of the richness of their environments (Charnov, 1976, Krebs et al., 1977). An alternative view posits that instead of focusing on the constant present, animals and humans should base their choices on the near future (McNamara, 1982). In short, McNamara’s idea was that animals and humans should estimate the potential of a patch to yield sufficient payment in the near future. While these “potential functions” allow flexibility under uncertainty by being informed by any environmental priors and taking diverse functional forms, they were initially vaguely defined (as admitted by McNamara himself). However, a recent model more precisely addressed the problem of uncertainty by combining elements from drift-like evidence accumulation and MVT rules (Davidson & Hady, 2019). This “Foraging Drift Diffusion Model” (FDDM) treats time within a patch as an evidence accumulation process, and can be parameterized similar to DDM models described above (e.g. Bogacz et al., 2006; Brunton et al., 2013). The authors show that by controlling the rate and direction of the accumulation process, as well as the location of the threshold, they can model behaviors that include counting for preys, waiting until certain amount of time has passed, or extending persistance as new preys are encountered. The various accumulation behaviors presented can be at least partially reproduced by tweaking the parameter lambda in traditional DDM (leak vs perfect memory in Brunton et al., 2013; O-U models in Bogacz et al., 2006). Incorporating evidence acumulation models into foraging scenarios is not new, as Calhoun et al (2014) have demonstrated that the precise information-maximizing foraging pattern of C. Elegans (e.g. center-surround systematic investigation based on short turns, with sudden patch exiting) can be efficiently computed using DDM and very few interneurons (although it is worth remembering that single neurons are unlikely to compute the evidence trace by themselves, per Scott et al., 2017).
While both current and future-oriented processes can explain patch foraging behavior, a way to determine which one is actually used is to probe how subjects learn the statistics of the environment. Constantino & Daw (2015) looked into this question by comparing the performance of MVT against temporal difference (TD) learning algorithms in predictable and stochastic environments in humans.
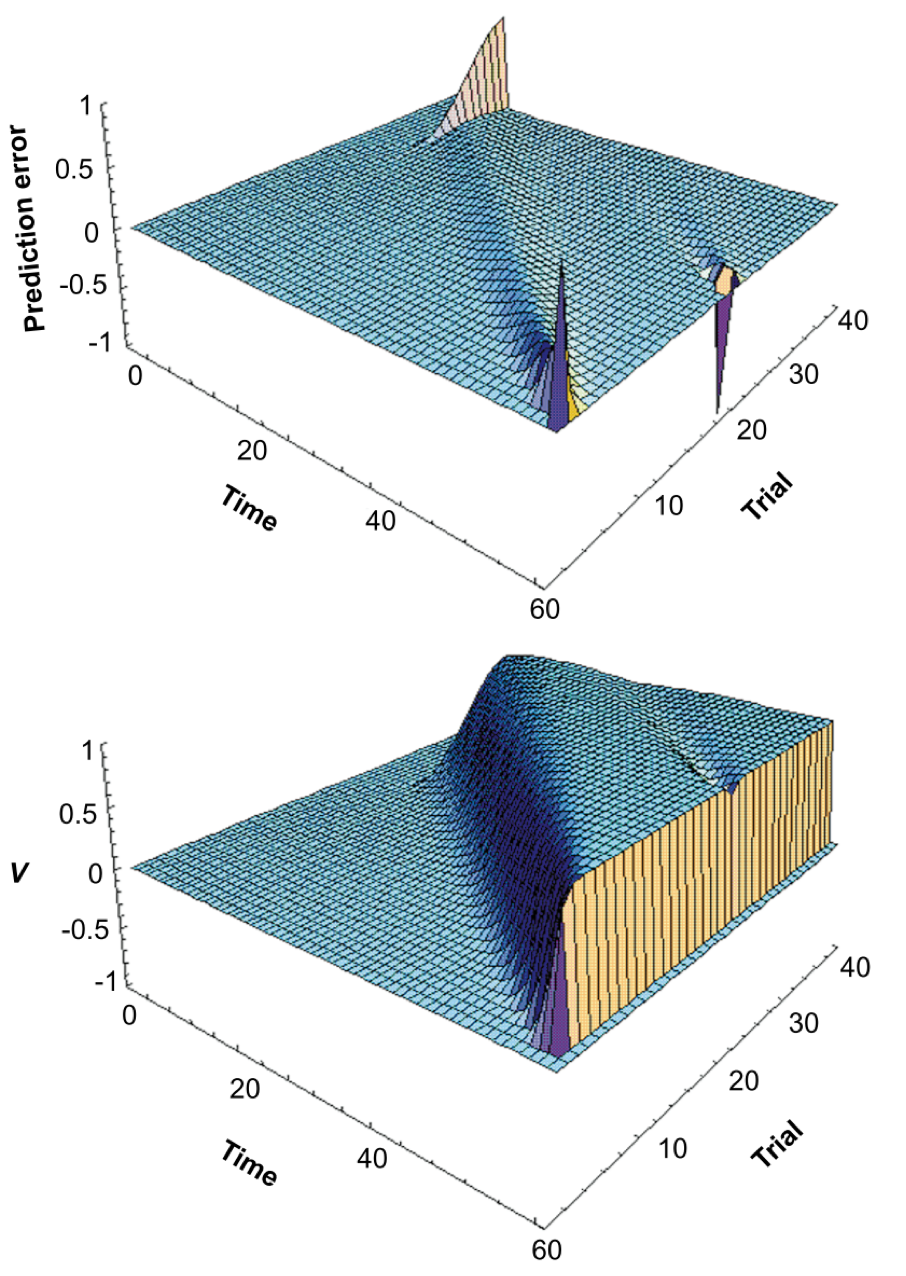
TD algorithms fall under the reinforcement learning (RL) category, but unlike state-outcome pairings of traditional RL, they learn pairings based on the predictive outcome of neighboring states (Sutton 1988). Updating states based on expected consecutive ones provides flexibility and efficiency to the algorithm, depending on how far the discounting eligibility trace reaches (these discounted traces, paramaterized by lambda, embody how far out in time a state’s predictive power reaches). Alternative, more efficient models rely on mapping spatial transitions that allow quick updating of reward distributions (see successor representations, explained by Gershman 2018). TD-lambda models have been informative in explaining neuroscientific phenomena. For example, dopaminergic neurons become active when unexpected rewards occur, and slowly transition their activity to stimuli that reliably predict these rewards over time (and reduce their firing when learned expected rewards are omitted). Schultz et al (1997) noted that these reward prediction error dynamics resemble the slow transitions from outcome to early predictors produced by TD (see figure below, from their paper). O’Doherty et al (2003) similarly showed that the BOLD-fMRI response in human orbitofrontal cortex (OFC) and striatum during classical conditioning learning (unconditional to conditional stimuli transitions) can be modeled using TD-based RL predictors. Interestingly, OFC has been observed to track the confidence rats have in their perceptual evidence accumulation decisions (Lak et al., 2014), and supports higher order, model-based processes required for decisions involving multiple steps in the future (Miller, Botvinick, & Brody, 2017) (engaging in model-based behavior also depends on locus coeruleus activity to ACC, per Tervo et al., 2014).
These neuroscientific results indirectly connect TD-lambda learning to evidence-accumulating and future-oriented factors that were suggested above to participate in foraging decisions (McNamara, 1982; Calhoun et al., 2014; Davidson & Hady, 2019), providing support to their use as foragers learn the statistics of the environment. However, what Constantino & Daw (2015) found was that humans learn these statistics in line with MVT estimates instead. This means that the instantaneous rate of rewards governs choices even in stochastic environments, going beyond the predictions of Charnov’s normative model.
Collectively, these findings show that even if computational models can be combined to explain various decision making scenarios, there are unique benefits afforded to each. Unfortunately the literature explained here is limited to a very small corpus, and other available lines of thought might be able to explain the gaps seen here. Regardless, future work might yet be able to further mix these lines of evidence in a way that can flexibly explain choice-related observations ranging from neural to behavioral.
References
Bogacz, R. (2006). The physics of optimal decision making: A formal analysis of models of performance in two-alternative forced choice tasks, Psychological Review, 113(4), 700-765
Brunton, B. W., Botvinick, M., & Brody, C. D. (2013). Rats and Humans Can Optimally Accumulate Evidence for Decision-Making. 340(April), 95–99.
Calhoun, A. J., Chalasani, S. H., & Sharpee, T. O. (2014). Maximally informative foraging by Caenorhabditis elegans. eLife, 2014(3), 1–13. https://doi.org/10.7554/eLife.04220.001
Charnov, E. L. (1978). Optimal foraging, the marginal value theorem. Theoretical Population Biology, 752(4), 739–752.
Constantino, S. M., & Daw, N. D. (2015). Learning the opportunity cost of time in a patch-foraging task. Cognitive, Affective & Behavioral Neuroscience, 15(4), 837–853. https://doi.org/10.3758/s13415-015-0350-y
Constantinople, C. M., Piet, A. T., & Brody, C. D. (2019). An Analysis of Decision under Risk in Rats. Current Biology, 29(12), 2066–2074.e5. https://doi.org/10.1016/j.cub.2019.05.013
Davidson, J. D., & El Hady, A. (2019). Foraging as an evidence accumulation process. PLOSComputational Biology, 15(7), e1007060. https://doi.org/10.1371/journal.pcbi.1007060
Fawcett, T. W., McNamara, J. M., & Houston, A. I. (2012). When is it adaptive to be patient? A general framework for evaluating delayed rewards. Behavioural Processes, 89(2), 128–136. https://doi.org/10.1016/j.beproc.2011.08.015
Gershman, S. J. (2018). The successor representation: Its computational logic and neural substrates. Journal of Neuroscience, 38(33), 7193–7200. https://doi.org/10.1523/JNEUROSCI.0151-18.2018
Krajbich, I., & Rangel, A. (2011). Multialternative drift-diffusion model predicts the relationship between visual fixations and choice in value-based decisions. Proceedings of the National Academy of Sciences of the United States of America, 108(33), 13852–13857. https://doi.org/10.1073/pnas.1101328108
Krebs, B. Y. J. R., Erichsen, J. T., & Webber, M. I. (1977). Optimal prey selection in the great tit (Parsus major). Animal Behavior, 25(2), 30–38.
Krebs, J. R., & Kacelnik, A. (1984). Time Horizons of Foraging Animals. Annals of the New York Academy of Sciences, 423(1), 278–291. https://doi.org/10.1111/j.1749-6632.1984.tb23437.x
Lak, A., Costa, G. M., Romberg, E., Koulakov, A. A., Mainen, Z. F., & Kepecs, A. (2014). Orbitofrontal cortex is required for optimal waiting based on decision confidence. Neuron, 84(1), 190–201. https://doi.org/10.1016/j.neuron.2014.08.039
Louie, K., Khaw, M. W., & Glimcher, P. W. (2013). Normalization is a general neural mechanism for context-dependent decision making. Proceedings of the National Academy of Sciences of the United States of America, 110(15), 6139–6144. https://doi.org/10.1073/pnas.1217854110
McNamara, J. (1982). Optimal patch use in a stochastic environment. Theoretical Population Biology, 21(2), 269–288. https://doi.org/10.1016/0040-5809(82)90018-1
Miller, K. J., Botvinick, M. M., & Brody, C. D. (2017). Dorsal hippocampus contributes to model-based planning. Nature Neuroscience, 20(9), 1269–1276. https://doi.org/10.1038/nn.4613
Niv, Y., Daw, N. D., Joel, D., & Dayan, P. (2007). Tonic dopamine: Opportunity costs and the control of response vigor. Psychopharmacology, 191(3), 507–520. https://doi.org/10.1007/s00213-006-0502-4
O’Doherty, J. P., Dayan, P., Friston, K., Critchley, H., & Dolan, R. J. (2003). Temporal Difference Models and Reward-Related Learning in the Human Brain John. Neuron, 28, 329–337. https://doi.org/10.1016/S0896-6273(03)00169-7
Roitman, J. D., & Shadlen, M. N. (2002). Response of neurons in the lateral intraparietal area during a combined visual discrimination reaction time task. Journal of Neuroscience, 22(21), 9475–9489.
Schultz, W., Dayan, P., & Montague, P. R. (1997). A neural substrate of prediction and reward. Science, 275(5306), 1593–1599.
Scott, B. B., Constantinople, C. M., Akrami, A., Hanks, T. D., Brody, C. D., & Tank, D. W. (2017). Fronto-parietal Cortical Circuits Encode Accumulated Evidence with a Diversity of Timescales. Neuron, 95(2), 385–398.e5. https://doi.org/10.1016/j.neuron.2017.06.013
Sutton, R. S. (1988). Learning to Predict by the Methods of Temporal Differences. Machine Learning, 3(1), 9–44. https://doi.org/10.1023/A:1022633531479
Tervo, D.G., Proskurin, M., Manakov, M., Kabra, M., Vollmer, A., Branson, K., & Karpova, A. Y. (2014). Behavioral variability through stochastic choice and its gating by anterior cingulate cortex. Cell, 159(1), 21–32. https://doi.org/10.1016/j.cell.2014.08.037
Wikenheiser, A. M., Stephens, D. W., & Redish, A. D. (2013). Subjective costs drive overly patient foraging strategies in rats on an intertemporal foraging task. Proceedings of the National Academy of Sciences, 110(20), 8308–8313. https://doi.org/10.1073/pnas.1220738110
Zimmermann, J., Glimcher, P. W., & Louie, K. (2018). Multiple timescales of normalized value coding underlie adaptive choice behavior. Nature Communications, 9(1), 1–11. https://doi.org/10.1038/s41467-018-05507-8